En praktisk implementasjon av tapsfri kompresjon i HEVC

Denne artikkelen beskriver et design av en h.265 entropi koder utført som en masteroppgave på instituttet for elektroniske systemer på Norges teknisk-naturvitenskapelige universitet, høsten 2017.

HEVC bygger på det enkle prinsippet at mye av denne videodatamengden er redundant.  De fleste farger dekker mer enn bare en pixel, og det finnes mange mønster i bildet som gjentar seg. Dette gjør at man i stedet for å sende hele nye bilder, kan sende forskjellen mellom hvert bilde. Når man i tillegg kan drastisk redusere mengden data som må sendes for hvert originale bilde, så oppnår man en ekstremt høy kompresjonsrate. Denne mønstergjenkjenningen er ikke det eneste trikstet som HEVC utnytter. De fleste kjenner til hvordan det er mulig å komprimere data ved å bruke for eksempel ZIP eller RAR. Dette er komprimerings- og arkiveringsfilformat som brukes for effektiv og tapsfri lagring og transport av data. Det samme prinsippet benyttes i HEVC, hvor Context Adaptive Binary Arithmetic Coding (CABAC) brukes for entropi (tapsfri) kompresjon.

Grunnen til at CABAC er benyttet i HEVC er at den oppnår kompresjon som nærmer seg den teoretiske grensen. Kostnaden for denne ytelsen er en meget høy
beregningsmessig kompleksitet. Algoritmen er også veldig sekvensiell og baserer seg på behandling av et enkelt bit om gangen. Dette er ting som gjør den meget interessant med tanke på en eventuell hardware implementasjon. Det har også lenge eksistert offentlige software implementasjoner, men HEVC i hardware har ikke sett lignende eksempler. Med den store akademiske interessen for CABAC, vil en praktisk implementasjon være et nyttig bidrag. Dette har vært hovedmotivasjonen for min masteroppgave hvor en HEVC kompatibel FPGA implementasjon av CABAC har blitt analysert og utviklet i VHDL.

Prinsippene bak CABAC
Hvordan dette CABAC systemet henger sammen, kan fort bli komplisert og uoversiktlig, men de geniale prinsippene bak funksjonen er en del enklere å forstå. Aritmetisk koding slekter på den mer kjente entropikode-metoden Huffman-koding. Denne kodingen har blitt mye benyttet i tidligere videostandarder, hvor den har vært kjent som Context-Adaptive Variable Length Coding (CAVLC). Denne metoden krever betydelig mindre prosessering enn CABAC, men oppnår ikke like god kompresjon. Huffman-koding fungerer prinsipielt ved at man tildeler kortere kodeord for symboler som oppstår oftest i et sett med data

Aritmetisk-koding skiller seg fra Huffman-koding ved at man i stedet for å tildele symbolene en kode direkte, så tildeler man hvert symbol en region mellom 0 og 1. Størrelsen på disse regionene er direkte basert på sannsynlighetsmodellen.

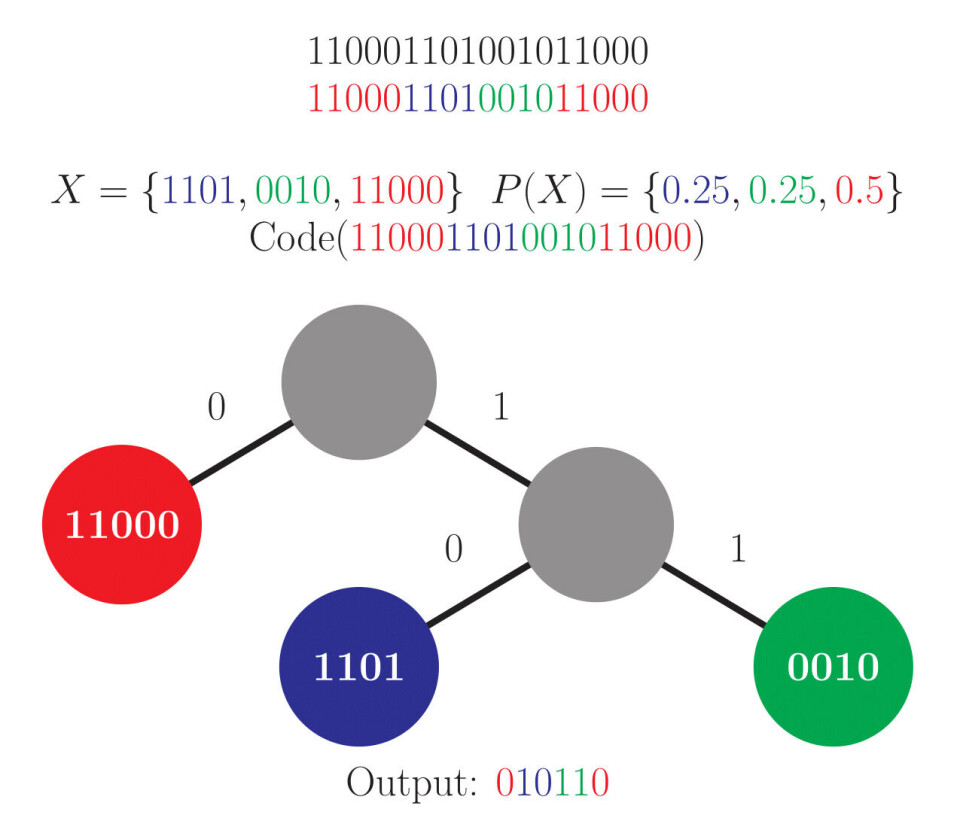
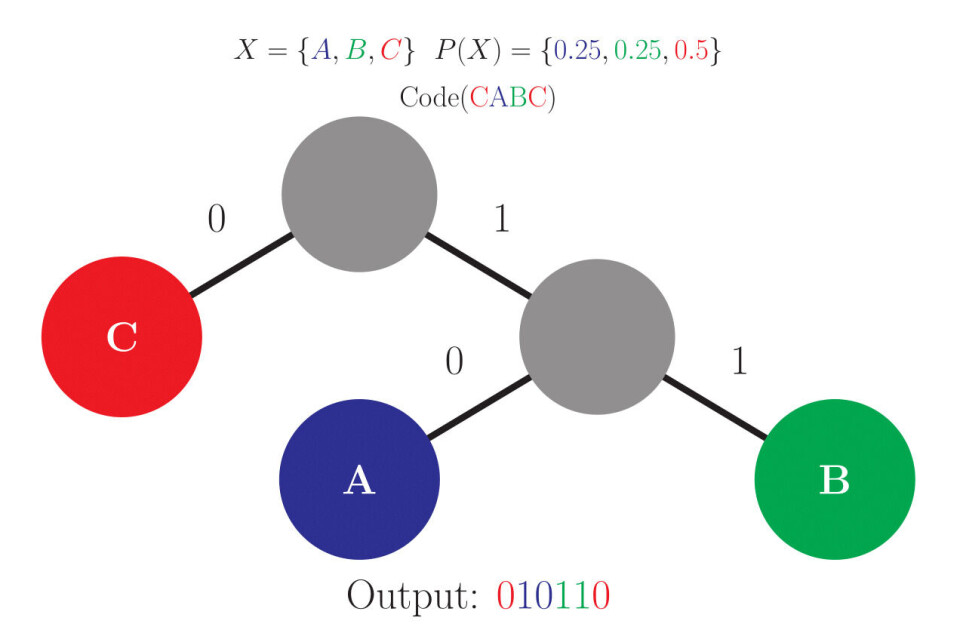
Aritmetisk-koding skiller seg fra Huffman-koding ved at man i stedet for å tildele symbolene en kode direkte, så tildeler man hvert symbol en region mellom 0 og 1. Størrelsen på disse regionene er direkte basert på sannsynlighetsmodellen.

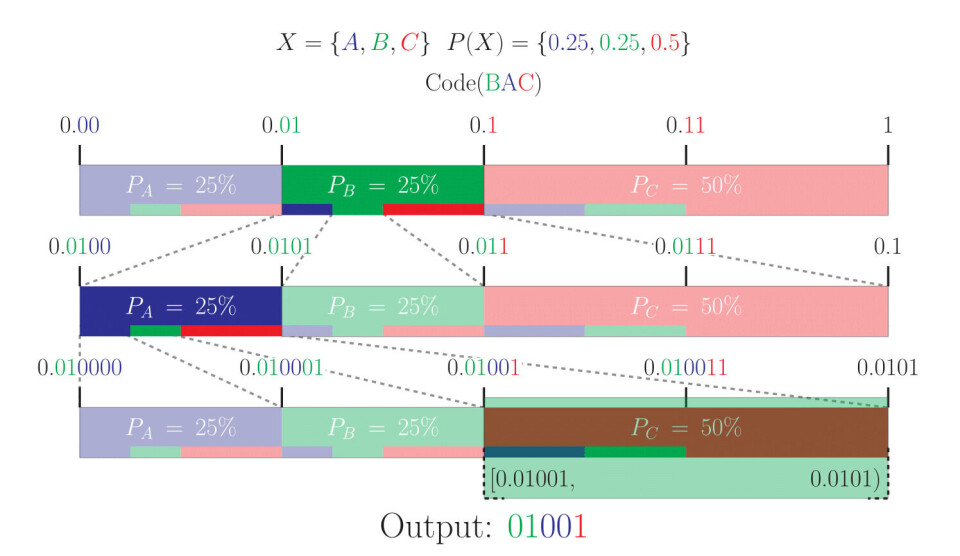
Med dette utgangspunktet er det mulig å representere et hvert symbol som et desimaltall mellom 0 og opp til, men ikke inklusiv 1, siden alle disse tallene vil falle på en unik region. Dermed kan man sende det kortest mulige tallet som befinner seg i regionen til symbolet man vil sende, og mottakeren vil kunne forstå hvilket symbol man henviser til ved å se hvilken region tallet ligger i.

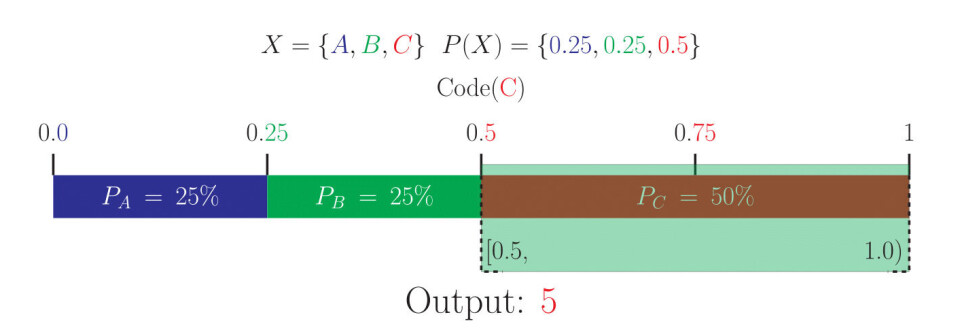
Siden vi er ute etter å finne den optimale representasjonen i binær form, kan det være nyttig å representere regionene med binære tall direkte. Dette har også en bonuseffekt i at man kan finne tilnærmet optimale representasjoner ved å sende det nederste tallet i regionen.

Flere symboler kan kodes ved at man først koder et symbol, og så gjentar prosessen inne i regionen til det først enkodede symbolet, hvor denne nye regionen blir delt opp på samme måte. Dette er hovedgrunnen til at CABAC algoritmen er så sekvensiell, siden hver nye regionsoppdeling er avhengig av den forrige.

For å finne tilbake til symbolene som har blitt sendt putter man helt enkelt det binære tallet man har fått tilsendt, inn i den samme modellen. Man vil da kunne lese ut alle symbolene ved å se hvilke regioner dette tallet henviser til.

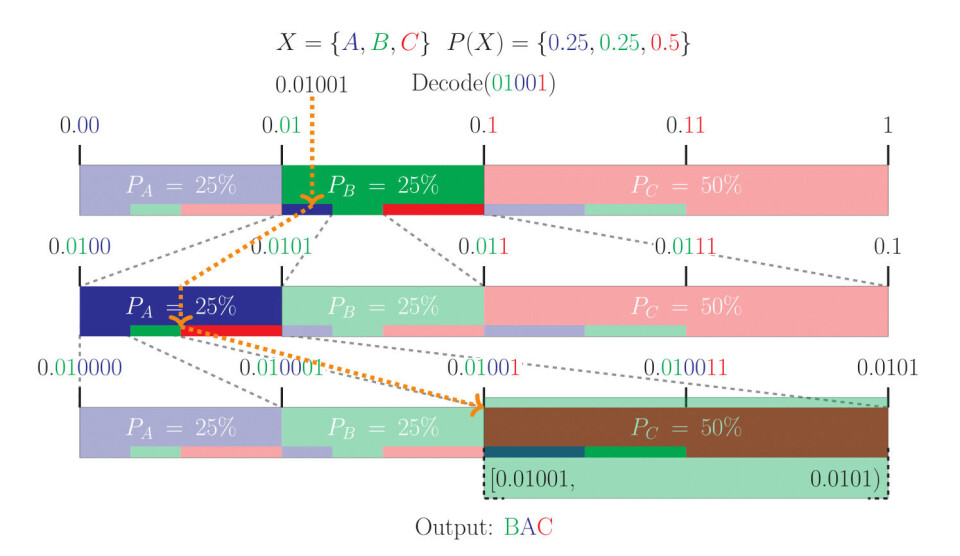
Selv om  aritmetisk-koding kun dekker to av bokstavene i Context-Adaptive Binary Arithmetic Coding (CABAC), er det den mest kompliserte og viktigste delen. Det at den er adaptiv, viser til bruken av sannsynlighetsmodeller som dynamisk endrer sannsynligheten til hvert symbol, ut ifra hvor ofte det er observert. Dette er videre optimalisert ved å bruke forskjellige kontekster (sannsynlighetsmodeller) ut ifra hvilken type data som blir kodet. Binær aritmetisk-koding er en spesiell form for aritmetisk-koding hvor man kun bruker “0” og “1” som symboler, og derfor kun trenger sannsynlighetsmodell for 2 symboler. Dette har betydning for den praktiske implementasjonen, men prinsippene er de samme som er forklart over.

Implementasjonen
Den største utfordringen i utviklingen av selve CABAC enkoderen i forbindelse med masteroppgaven, var å sørge for å følge alle reglene i HEVC. Dokumentasjonen beskriver kun en ren software implementasjon av en CABAC-koder og -dekoder. For å vite at man har laget en korrekt implementasjon, er man avhengig av en referanse som man er sikker på at er riktig. Den beste løsningen hadde kanskje vært å bruke den offisielle C++ HEVC test modellen direkte, men i oppgaven ble det heller utviklet en koder og dekoder i C#. Dette gjorde det mulig å verifisere at hardware koderen produserte gyldige data. Det var også en fin introduksjon til algoritmen, noe som gjorde det enklere å implementere i hardware.

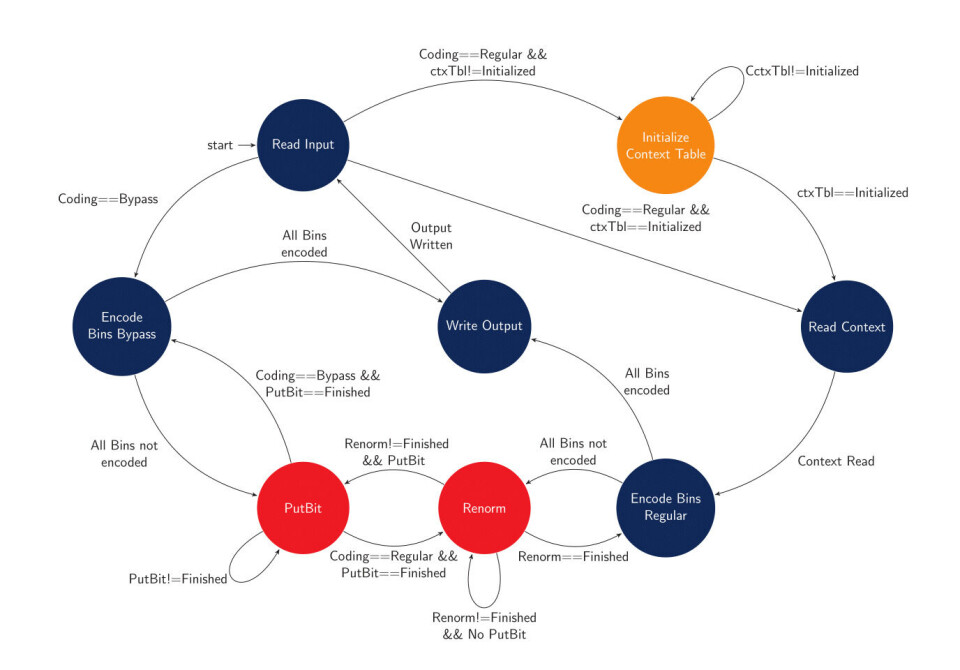
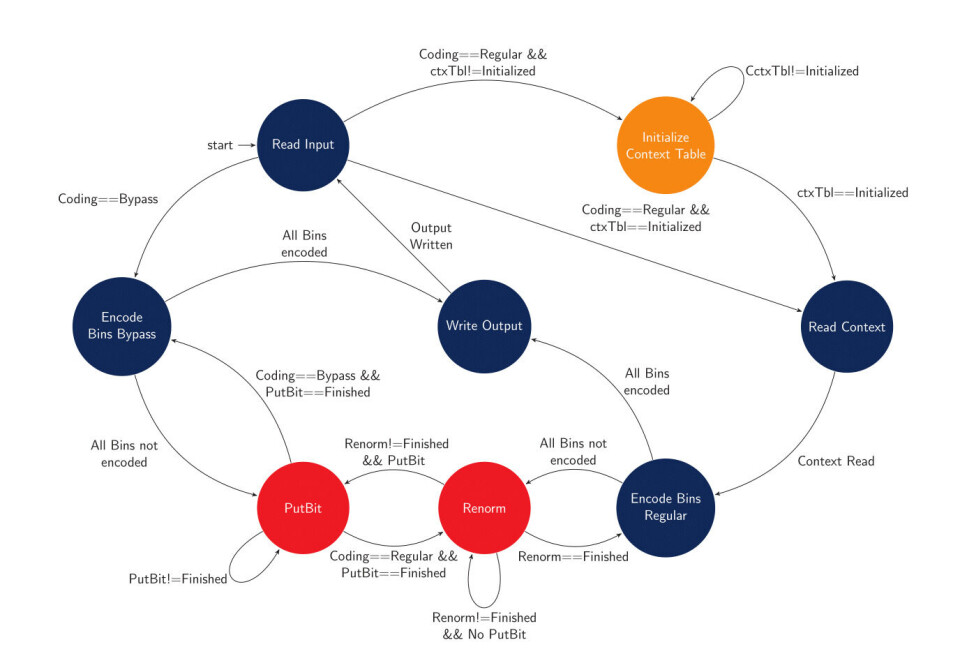
Hovedutfordringen for en effektiv hardware implementasjon ligger i algoritmens renormalisering og PutBit tilstander. I software er disse tilstandene implementert som while-loops med ukjent kjøretid. Dette fører til at et eventuelt pipelinet design må kunne stoppe og gjøre seg ferdig med disse tilstandene. Hardware koderen kan konfigureres til å takle flere iterasjoner av putbit-tilstanden hver klokkesyklus, men dette har en drastisk påvirkning på den potensielle maksfrekvensen. Renormalisering vil  kreve en hel klokkesyklus for hver iterasjon. En effektiv løsning av disse problemene vil føre til en drastisk økning i ytelse. Initialisering av konteksttabeller vil også bidra til mindre datagjennomstrømming, men dette er det mulig å parallellisere.

Den nåværende implementasjonen kan håndtere rundt 20Mb/s syntetisert på ZYNQ-7000(28nm Artix®-7 ), med under 6% FPGA-utnyttelse. Dette er kun nok til å dekke lavere nivåer av HEVC profiler (Standard Definition og lavkvalitets High Definition video), men det vil være tilstrekkelig til for eksempel live-streaming av HD-Video.

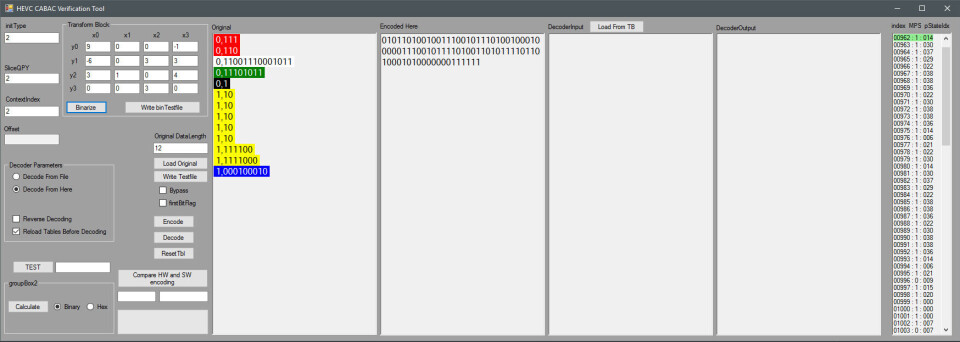
På grunn av den ekstremt høye beregningstiden for CABAC, er det benyttet en forbehandlingsprosess hvor mye åpenbart overflødige data blir fjernet. Dette steget refereres oftest til som Binærisering. Dette har alltid vært et viktig steg for entropikoding i videostandarder, men den har fått en betydelig oppgradering i HEVC. Hvor binæriseringen av den mest forekommende dataen er blitt adaptiv. Dette gjør det mulig å finne tilnærmet optimale representasjoner av en spesiell type data. Denne representasjonen er faktisk så optimal at den normale CABAC kode prosessen kan omgås. Noe som igjen fører til en drastisk reduksjon i tiden det tar å entropikode en video. Binæriserte data som omgår den normale koderen, blir aritmetisk-kodet ved å bruke en sannsynlighetsmodell med lik sannsynlighet for alle symboler. Dette refereres til som “bypass” koding og tar betydelig mindre tid å prosessere.

Fig 9: Figuren viser hvordan en matrise med 16-bits integer data blir oversatt til en minimert representasjon. Dette er en typisk operasjon for å binærisere transformasjonsdata som kommer i matriseformat. De binæriserte verdiene i oransje og gult benytter seg av den spesielt gode adaptive binæriseringsmetoden som er ny i HEVC. Den består av en sammensetning av k-th order Truncated Rice og k-th order Exp-Golomb koding. Hvor k- variabelen sørger for muligheten til å adaptivt optimalisere kodelengden.

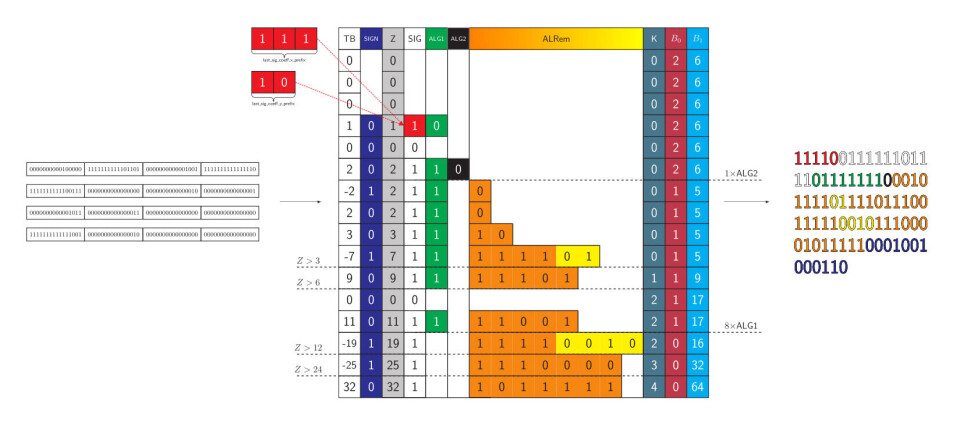
En betydelig mengde av arbeidet i oppgaven ble lagt ned i å finne en effektiv måte å implementere denne spesielle binæriseringsmetoden i hardware. Til slutt ble en svært effektiv løsning funnet. Den går ut på at det alltid finnes en sammensetning av Unary og Fixed-Length koding som er ekvivalent til sammensetningen av k-th order Truncated Rice og k-th order Exp-Golomb kodingen. I praksis vil dette innebære at man må behandle ethvert mulig spesialtilfelle. Siden variabelen k kun varierer mellom 0 og 4, er dette faktisk mulig i hardware. Denne metoden kan utføre denne binæriseringen for alle mulige verdier på kun en klokkesyklus.

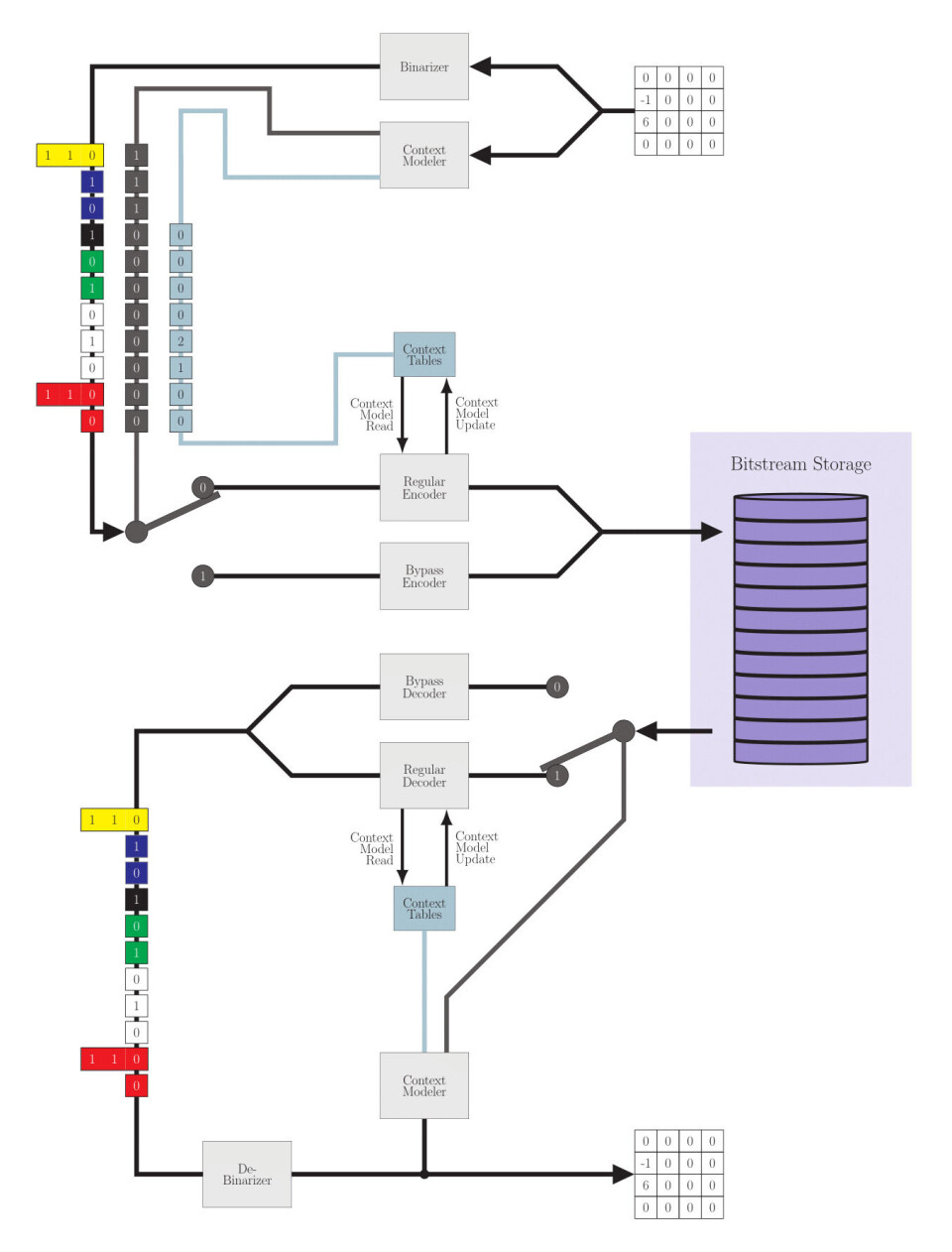
Avanserte videostandarder kan være ekstremt krevende å sette seg inn i. Uten den fantastiske oppfølgingen jeg har fått fra Postdoktor Milica Orlandic, hadde jeg ikke greid å gjennomføre denne oppgaven. Hennes kunnskap og formidlingsevner har vært helt uunnværlige. Jeg vil også takke Professor Kjetil Svarstad for veiledningen og innsikten han har gitt meg i verdenen av Hardware teori og design.

Referanser
Paulsen, Lars Erik Songe. Masteroppgave: "Design and analysis of an H.265 entropy encoder." (2017)